Реализация принципа индивидуального подхода при формировании вычислительных навыков

метки: Закрепление, Личной, Задание, Ученик, Получить, Математик, Ребенок, Знание

Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных умений и навыков, основу которых составляет осознанное и прочное усвоение приемов устных и письменных вычислений.

актуальность , Проблема

Отмечается ухудшение качества вычислений учащихся, обучающихся и по обычным, и по развивающим учебникам. Особенно пострадала культура устного счета. В настоящее время в реальной школьной практике возрастает количество детей, которые испытывают трудности в учёбе, требуют особого внимания педагога.

актуальная тема , Цель исследования , Объект исследования , Предмет исследования , Гипотеза исследования , Задачи исследования

• проанализировать основные теоретические подходы в педагогической литературе, которые решают проблему обучения младших школьников основам вычислений;

• выбрать и апробировать образовательные технологии, основанные на индивидуальном и групповом подходах и направленные на формирование вычислительных умений и навыков младших школьников;

• подобрать методики диагностики и исследовать уровень сформированности вычислительных умений и навыков младших школьников;

• составить рекомендации для педагогов начальной школы по применению индивидуального подхода при обучении младших школьников основам вычислений.

Методы исследования , Методологическая основа исследования

Педагогические теории развивающего обучения (А.К.Артемов, А.Дисверг, К.Д. Ушинский, Л.С. Выгодский, Л.В. Занков, Д.Б. Эльконин, В.В.Давыдов).

Педагогические теории личностно – ориентированного обучения (Ш.А. Амонашвили, В.В. Беляев, В.С. Сухомлинский, И.С. Якиманская и др.).

Психологические теории, раскрывающие особенности детей младшего школьного возраста (В.С. Мухина, Д.Б. Эльконин).

Исследование закономерностей становления представлений о числе, развития счетной деятельности, вычислительной деятельности (А.М. Леушина, Н.Г. Бакст, Т.В. Тарунтаева, В.В. Данилова, Г.А. Корнилова, Т.Д. Рихтерман).

«Орфографические ошибки младших школьников и пути их предупреждения ...

... работы, от обучения графике, от формирования у школьников графических умений и навыков. Правила орфографии определяют выбор написаний в следующих пяти областях письма, в ... навыка у младших школьников Русский язык ... в словах: правила правописания безударных гласных в корнях слов, в приставках и других морфемах; звонких и глухих согласных в слабых позициях, в корнях слов и других ... опасность ошибки. К ним ...

Практическая значимость исследования , База исследования , Структура и объем работы , Апробация

1. Умерова Ю.В., Гаврилина О.В. Особенности формирования вычислительных навыков у младших школьников в процессе учебной деятельности //Традиции и инновации в педагогике начальной школы, посвящённый 25-летию ГБОУВО РК КИПУ.-Симферополь : ИТ «АРИАЛ»,2018.-410с-С.292-294.

2. Умерова Ю.В., Гаврилина О.В. Формирование вычислительных навыков на уроках математики в начальной школе //Педагогические и социологические аспекты образования. Материалы Международной научно-практической конференции. 2018.,С.187-188. Статья РИНЦ.

1.1 Общая характеристика формирования вычислительных навыков у младших школьников

Основу вычислительной составляющей математической компетентности образует готовность ученика применять вычислительные умения и навыки в практических ситуациях. В смысле начального математического образования в их число, в частности, относят умение сравнивать числа, выполнять арифметические действия с ними; находить значения числовых выражений; сравнивать значение одноименных величин и выполнять действия с ними и тому подобное.

Вопрос о формировании вычислительных навыков большинство методистов рассматривает с точки зрения разнообразия упражнений на вычисление.

При изучении сложения и вычитания двузначных чисел без перехода через разряд главным является сосредоточение внимания на способах выполнения этих действий, на вычислительных приемах.

В рамках данной темы используются приемы, теоретической основой которых является правило сложения числа к сумме или правило вычитания числа от суммы. Таким образом, в рамках этой темы используются приемы поразрядного сложения и вычитания и прием сложения и вычитания частями.

Анализ способов сложения и вычитания чисел в пределах 100 без перехода через разряд свидетельствует, что для их сознательного выполнения ученики должны хорошо знать нумерацию чисел в пределах 100, таблицы сложения одноцифровых чисел в пределах 10 и соответствующие случаи вычитания и усвоить правила, которые являются теоретической основой приемов вычисления.

Рейс по маршруту (Переход из Клайпеде в порт Скаген через пролив Зунд)

...  303 Таблица 13. РТС, НО по маршруту перехода № по РТ СНО Наименование Позывной Частота Время работы 6395 п. Скаген Skagen-1 ... порт Скаген, при необходимости в процессе прохода судна по маршруту можно произвести расчеты для любой требуемой точки), а ... 6.82 Заключение Целью данного курсового проекта являлась проработка перехода судна по заданному маршруту с учетом реальных условий и обстоятельств, что ...

В действующих учебниках по математике для начальной школы реализованы разные подходы, по разработке темы «Сложение и вычитание двузначных чисел в пределах 100 без перехода через разряд», которые позволяют выделить основные их отличия.

Первое отличие методических систем касается порядка изучения случаев сложения и вычитания в пределах 100 без перехода через разряд.

По учебнику Л. Кочиной сложение и вычитание двузначных чисел изучается в следующем порядке:

1. случаи сложения и вычитания вида: 45 + 2, 45 + 20 45-2, 45-20;

2. случаи добавления вида: 56 + 4

3. случаи сложения и вычитания вида: 34 + 52, 76-44 (частями);

4. сложение и вычитание вида: 34 + 52, 76-44 (поразрядно).

По учебнику М. Богдановича сначала рассматриваются общие случаи сложения и вычитания двузначных чисел, а затем — частные.

Второе отличие заключается в том, что по системе Л. Кочиной, методика изучения сложения и вычитания двузначных чисел рассматривается на основе одновременной обработки взаимно обратных действий (сложение и вычитание), а по системе М. Богдановича — на основе последовательного изучения сначала прибавление, а затем вычитание.

По мнению Скворцовой С.А., целесообразно использовать такую ​​последовательность введения случаев вычисления, когда ребенок движется от более простого к более сложному. Также, следуя принципам теории укрупнения дидактических единиц, а именно: одновременного изучения взаимно обратных действий, предлагаем следующую последовательность изучения случаев сложения и вычитания двузначных чисел без перехода через разряд [4]:

• прибавление (вычитание) однозначного числа к (от) двузначного без перехода через разряд;

• добавление (вычитание) круглого числа до (от) двузначного;

• поразрядное сложение и вычитание двузначных чисел без перехода через разряд;

• сложение и вычитание частями;

• добавление удобным способом.

В результате освоения темы ученик должен овладеть вычислительными приемами сложения и вычитания двузначных чисел без перехода через десяток (поразрядное сложение и вычитание, сложение и вычитание частями), вычислять сумму и разность двузначных чисел различными способами.

Исходя из возрастных особенностей протекания познавательных процессов младших школьников, с целью формирования полноценных вычислительных навыков в добавлении и вычитании двузначных чисел без перехода через разряд, следует использовать наглядный материал, а именно:

• пучки палочек (десятки) и отдельные палочки (единицы);

• стержни бусинок (десятки) и отдельные бусинки (единицы);

• бруски кубиков (десятки) и отдельные кубики (единицы);

• плакаты с содержанием приемов вычисления — памятники;

• таблицы с разрезными карманами — схемы способов вычисления, карточки с печатной основой.

Также формированию вычислительных навыков способствуют математические Монтессори-материалы — отдельные бусинки, иллюстрирующие единицы и стержни из 10 бусин-десятки. Кроме того, в методике Монтессори используются карточки разных цветов: синим записаны одноцифровые числа, зеленым — круглые десятки. Обозначая карточками числа, изображено стержнями и отдельными бусинками, дети сначала кладут карточку с круглым числом, означает количество десятков, а затем на «ноль» кладут карточку с числом единиц [5].

На современном этапе развития начального математического образования необходимо выбрать такие способы организации вычислительной деятельности младших школьников, которые будут способствовать не только формированию прочных осознанных вычислительных умений и навыков, но и всестороннему развитию личности ученика.

» Методика формирования устных вычислительных навыков в ...

... способы организации вычислительной деятельности школьников, которые способствуют не только формированию прочных вычислительных умений и навыков, но и всестороннему развитию личности ребенка. При выборе способов организации вычислительной деятельности необходимо ориентироваться на развивающий характер работы, отдавать ...

При выборе способов организации вычислительной деятельности приоритетными должны быть знания доминирующей познавательной мотивацией, ориентацией на развивающий характер работы, с учетом индивидуальных особенностей ребенка и личный жизненный опыт.

К эффективному учебно-воспитательному процессу усвоения ребенком вычислительных умений и навыков осуществляется в единстве с всесторонним развитием его личности. Развивающим является не всякое обучение, а лишь то, которое не только учитывает доступное ребенку в процессе самостоятельной деятельности, но и ориентированное на «зону ближайшего развития», то есть на то, что ребенок может выполнить под руководством и с помощью взрослых.

Дети усваивают знания в различных видах деятельности, особенно во время обучения. Систематическое усвоение основ математики обогащает детей новыми знаниями, значительно расширяет их кругозор, предоставляет новый смысл их психической деятельности, перестраивая характер мыслительных процессов — восприятия, памяти и мышления, качественно меняя общую направленность и черты личности.

Развитие мышления учащихся — одна из важных задач математики в начальных классах, решение которой может быть осуществлено посредством формирования соответствующих операций (анализ, синтез, сравнение, обобщение и т.д.).

Диагностируя и проявляя проблемные моменты в усвоении вычислительных знаний, умений и навыков учащихся, стоит акцентировать внимание на индивидуальных свойствах личности, обусловливающие, в частности, продуктивность мышления, его творческий характер, глубину и широту, гибкость мышления.

Неправильно образующиеся ребенком ассоциации часто мешают осознать существенные признаки основных понятий. Чтобы это предотвратить, следует давать детям больше упражнений, где такие же слова и выражения связанные с арифметическими действиями.

Ученики быстрее учатся конкретизировать арифметические действия, если в обучении их этой операции придерживаться определенной последовательности.

Арифметика натуральных чисел – основное содержание курса математики 1-4 классов. На данном этапе, ставятся задачи сформировать у учащихся представление о натуральном числе и десятичную систему счисления, добиться усвоения содержания и приемов выполнения арифметических действий, выработать прочные вычислительные навыки и тому подобное.

«Современные образовательные технологии в обучении иностранному языку»

... процесс обучения детей игры и игровые моменты, учитель всегда должен помнить, что за игрой стоит урок – это знакомство с новым материалом, его закрепление и повторение, это и работа с учебником и ...

Работа над нумерацией и арифметическими действиями строится в начальном курсе концентрическая.

.

Знакомясь с программным материалом, учитель выбирает различные формы таких задач, которые следует использовать для достижения различных целей:

• для усвоения таблиц арифметических действий;

• упражнения на формирование вычислительных навыков;

• математические диктанты как одна из форм устных вычислений;

• задачи на усвоение вопросов теории арифметических действий;

• устные упражнения по геометрии;

• задачи с логической нагрузкой;

• творческие задачи.

Овладение учащимися указанными составляющими компетенции в системе обеспечивает формирование у них предметной математической компетентности как целостного личностного образования. Разработка методики этого процесса — перспективная проблема теоретиков и практиков начального обучения.

1.2. Сущность, принципы и организация индивидуального подхода к учащимся на уроках математики

В первую очередь необходимо разобраться, что же такое индивидуальность вообще и какую роль она играет в учебном процессе. Каждый человек индивидуален, так как это личность с ярко выраженным, особенным характером и внутренним миром. Индивидуальность характеризуется совокупностью интеллектуальных, волевых, моральных, социальных и других черт личности, которые заметно отличают данного человека от других людей. На Земле нет двух совершенно одинаковых людей. Каждый человек единственный и неповторимый.

«К индивидуальным особенностям человека можно отнести: своеобразие ощущений, восприятия, мышления, памяти и воображения; особенность интересов, склонностей, способностей, темперамента, характера личности» [7, с. 279].

Методика проведения занятий по спортивному туризму с учениками начальных классов

... разработать методику проведения занятий по спортивному туризму с учениками начальных классов. В соответствии с поставленной целью необходимо решить следующие задачи:  Изучить теоретико-методологические основы становления и классификации спортивного туризма.  Разработать методику физического воспитания учеников начальных классов средствами спортивного туризма.  Провести диагностику уровня ...

Следовательно, учебно-воспитательный процесс должен максимально опираться на индивидуальность. «Индивидуальный подход заключается в управлении человеком, основанном на глубоком знании черт его личности и его жизни. Индивидуальный подход создает наиболее благоприятные пути для развития активности, склонности и дарований каждого ученика. В индивидуальном подходе особенно нуждаются отстающие ученики , а также с ярко выраженной задержкой развития» [9, c .52].

Задача изучения данной проблемы состоит в том, чтобы сократить количество неуспевающих и запущенных детей.

Подобно тому, как различают по своим физическим качествам, говорил Василий Александрович Сухомлинский, так неодинаковы силы, необходимые для умственного труда. Память, наблюдательность, воображение, мышления не только по их глубине, устойчивости, быстроте протекания, но и в качественном отношении имеют индивидуальную характеристику у каждого школьника.

Большое внимание у В.А. Сухомлинского обращено на слабоуспевающих дет . Он показывает их недостатки – неразвитость умственных способностей: неустойчивость внимания и памяти, неразвитость мышления, бедность речи, не любознательны, неразвитость эмоциональной сферы [31, c .432].

В основе индивидуальных различий лежат особенности свойств нервной системы, на основе которых формируется психическая жизнь личности, все ее психические процессы, ее особенное и индивидуальное.

Особого внимания требуют индивидуальные особенности неуспевающих и недисциплинированных детей, в этом и помогает построение учебного процесса с точки индивидуально-группового подхода.

Таким образом, индивидуальный подход в современном мире очень важен. Каждый педагог должен владеть знаниями о психологических особенностях детей, проследить успеваемость под призмой этих знаний, чтобы индивидуально подойти к обучению каждого ребенка. В своей работе я хотела бы полностью развернуть вопрос индивидуального подхода в системе образования, в общем, и на уроках математики в частности, рассмотреть такие вопросы, как формирование вычислительных умений и навыков.

Образование в современном мире должно способствовать всестороннему развитию личности каждого ребенка и создавать все условия для его творческой самореализации. Основная задача современного педагога — воспитывать учеников, учить эффективно применять в своей работе полученные знания, обучаться на протяжении всей своей жизни.

В школьной системе обучения всегда возникали вопросы с мотивацией детей к учебе, а также был постоянный поиск новых эффективных средств и методов обучения.

Экскурсия как форма обучения

... сборы экспонатов и составление гербария, коллекций. Экскурсия была выдвинута как форма обучения, как особый тип урока. Многие педагоги, ... ученикам и без сомнения верными. Осуществляя наглядное обучение, учитель, по мнению Коменского, должен придерживаться следующих важных правил: необходимо ... не отвечает всем условиям хорошего умственного воспитания детей, как натуральная история. В самой вещи: 1) ...

«К отрицательным моментам обучения можно отнести:

1. Отсутствие самостоятельного развития ученика.

2. Обучение детей и проведение уроков по одному шаблону, без учета способностей к восприятию и личных особенностей ученика.

3. Метод принуждения. Ученик – “обязан”, учитель – всегда прав. Минус такого обучения, большой минус, состоит в том, что чем сильнее давление на ребенка, тем больше вероятность отторжения и нежелания учиться.

4. Отсутствие внутренней мотивации к обучению. Ребенку нужно привить интерес к обучению, а не просто учиться потому, что нужно.

5. В процессе получения знаний нет нравственного развития личности ребенка» [29, c .212].

«Наше государство ставит перед школой задачи повысить качество обучения, воспитания и обеспечить более высокий уровень преподавания каждого предмета. Качество обучения в основном зависит от учителя и от его умения найти подход к каждому ученику, заинтересовать его своим предметом и развить в нем творческие способности.

Каждый ребенок обладает индивидуальными свойствами памяти, способностями к размышлению, имеет свой уровень темперамента и свои собственные интересы. В результате, не все учащиеся одинаково успешно усваивают материал, овладевают знаниями и приобретают необходимые навыки. Следовательно, чтобы максимально раскрыть способности каждого ученика, необходимо применять индивидуальный подход» [24, c .168].

Основные мотивы разработки и практического применения методов индивидуального подхода это:

1. Для успешного обучения нужно найти подход к каждому ученику.

2. Применить системный подход передачи знаний, дающий возможность ребенку принимать деятельное участие в процессе.

3. Разработать учебный процесс, по схеме совместной работы учителя и ученика и получить хорошие результаты обучения [35, c .79].

Индивидуальный подход к каждому ученику состоит в изучении во время учебного процесса личностных особенностей каждого ребенка, независимо от его успеваемости, стараться максимально развить его творческие и мыслительные способности, обеспечить всестороннего развития учащегося, раскрытие их талантов. Максимально исправить отрицательные качества, противоречащие требованиям общества.

Для индивидуального подхода учитель должен хорошо знать своих учеников. Педагог Константин Ушинский писал: «Чтобы воспитывать человека во всех его отношениях, нужно знать его во всех отношениях. При подходе к изучению ребенка необходимо выяснить, что он представляет собою сегодня, каким был раньше и чего можно ожидать от него завтра. То есть, необходимо проследить развитие ученика и увидеть перспективы. Именно в этом кроется секрет успеха индивидуального подхода в обучении и воспитании учащихся» [32, c .451].

Обучение школьников решению составных задач

... должна дать ученику работа при решении данной им задачи. Выступая в роли конкретного материала для формирования знаний, задачи дают возможность связать теорию с практикой, обучение с жизнью. Решение задач формирует у детей практические ...

Психологами было разработано большое количество программ для индивидуального обучения детей. Их объединяет одна общая мысль – для успешного взаимодействия с учеником необходимо узнать, как проходит его жизнь в семье, каково состоянием здоровья ребенка, определить готовность учиться в данном классе, его отношение к школе, умение работать самостоятельно и т.д.

По нашему мнению, учитывая особенности развития ученика, можно уверенно работать над формированием его личности.

«Именно математика в первую очередь защищает нас от обмана чувств и учит, что одно дело — как на самом деле устроены предметы, воспринимаемые чувствами, другое дело — какими они кажутся; эта наука даёт надёжнейшие правила; кто им следует — тому не опасен обман чувств» (Леонард Эйлер).

«Индивидуальный подход — это один из современных методов повышения качества обучения математике, при котором учитель контролирует знания каждого ребенка и может, в зависимости от индивидуальных способностей ученика принимать меры по их улучшению» [37, c .80].

Изложение учебной программы должно быть таким, чтобы стимулировать учащихся к самостоятельной работе.

«Метод индивидуального подхода предполагает:

• доверие и взаимопонимание между учителем и учеником;

• использование разнообразных форм общения, особенно диалога;

• учет индивидуальных особенностей каждого ребенка;

• обогащение собственного опыта детей;

• поощрение и стимулирование учеников к выбору домашних заданий и способов их выполнения;

• высказывание учащимися собственного мнения» [45, c .240].

Термин «дифференциация» (от латинского слова «различие») – значит необходимость «деления, структурирования, выделения частей».

«Дифференциация – вид организации обучения, при котором класс делится на отдельные группы, что позволяет сформировать у учеников чувство ответственности перед товарищами за результат совместной работы и при этом, дает возможность научиться самостоятельно принимать решения и отстаивать их правильность, а также приучает прислушиваться к мнению товарищей и вовремя исправлять допущенные ошибки. Поэтому дифференциация способствует формированию у детей самоконтроля и правильной самооценки» [48, c .35].

Целесообразно создавать группы детей в соответствии с их самооценкой. При этом в каждой группе предлагаются задания на выбор, что прививает учащимся самостоятельность и дает возможность оценить их уровень знания.

Основными принципами дифференциации являются:

• открытое предъявление учащимся своих достижений;

• последовательность в продвижении по уровням обучения;

• добровольности в выборе уровня учебного материала.

Итак, при принципе дифференциации ученик получает ценнейшее право – право выбора ограничиться начальным уровнем знаний или получить повышенную подготовку. Следовательно, задача учителя — организовать обучение на всех уровнях (начальный, достаточный, средний, высокий), а ученик выбирает доступный уровень знания именно ему. Это снижает нагрузку на детей, не могущих достичь высокого уровня. Уменьшается страх перед оцениванием знаний. Ученик имеет возможность получить знания по математике, которые необходимы именно ему.

А индивидуализация обучения — работа с каждым учеником отдельно, опираясь на знание его личных качеств, мотивации, интересов и способностей.

Получается, что в основе дифференциации обучения лежат различные программы, а в основе индивидуального подхода лежит внимание именно к отдельной личности и ее особенностям, содержание и объем программы при этом не меняется (Приложения 1 и 2) [51, c .53].

«Как показывает практика, в одном и том же классе разница в усвоении материала учениками может быть очень велика. В этом случае именно дифференциация дает наилучшие условия для полноценного развития способностей ребенка. И не являясь самоцелью, служит прекрасным средством для раскрытия способностей ученика.

При индивидуальном подходе можно применить различные варианты оценивания работ учеников. В первом варианте ученик сам выбирает уровень сложности заданий и выполняет задания этого уровня строго в течение отведённого времени. Во втором варианте — учащийся выполняет задания, с которыми он может справиться. При этом последовательность их выполнения выбирает сам. И третий — ученику предлагается задание, которое содержит несколько уровней сложности. Он сам определяет уровень, на котором будет выполнять задание, и применяет необходимые для данной работы знания» [46, c .218].

Затем следует провести анализ работ и сделать выводы об успешности освоения пройденного материала.

Индивидуальный подход означает пристальное внимание к каждому ребенку, изучение его интересов, уровня подготовки, умственных и физических возможностей.

Уровень знаний по математике у детей различен и, следовательно, учащиеся имеют разные способности к усвоению нового материала, поэтому учитель должен проводить уроки с учетом индивидуальных особенностей учеников.

«Сначала учитель формулирует основную суть проблемы и задает конечный результат. Учащиеся, зная результат, сами ищут пути решения.

Затем учитель указывает на существование проблемы, а учащиеся самостоятельно ищут решение, причем результат им неизвестен. И конечным этапом ученики самостоятельно находят проблему, сами формулируют ее и ищут ее решение.

Для подготовленных по математике и интересующихся ею ребят, умеющих мыслить самостоятельно, в проблемных заданиях с помощью индивидуальных карточек указывается конечная цель работы и прилагается информация об основных моментах, на которые необходимо обратить внимание при решении. Пути решения проблемы ученики ищут сами, но под контролем учителя.

Для более слабых учеников в карточках-заданиях подсказывается, какие именно операции нужно сделать для поиска решения задачи и описывается план действий, которые приведут к требуемому результату.

Учитель должен произвести тщательный анализ материалов урока:

1. Сравнить уровень сложности нового материала и навыки учеников.

2. Определить конкретные задачи, которые должны быть решены на уроке.

3. Методически подкрепить все этапы урока с учетом поставленных задач.

4. Проанализировать, какие сложности могут встретиться в ходе проведения урока, и быть готовым оказать помощь учащимся» [33, c .89].

Эффективность обучения математики с индивидуальным подходом можно оценить по следующим параметрам:

• успеваемость;

• желание учащихся усваивать новый материал;

• умение думать самостоятельно;

• повышение интереса учащихся к математике.

Домашние задания также необходимо давать индивидуально, учитывая уровень знаний и способностей каждого ученика. Сильным учащимся можно предлагать задачи, для решения которых придется творчески осмыслить и применить полученные на уроке знания. Слабые ученики в первую очередь нуждаются в приобретении умений и навыков, необходимых для решения простых задач.

Существует несколько видов контроля: урочно – традиционные, внеурочные, урочно – нетрадиционные (Приложения 3 и 4) [30, c .111].

1.3. Психолого–педагогические проблемы формирования вычислительных навыков и умений

При обучении ребенка в начальной школе, ребенок еще воспринимает цель взрослых как свою личную. Постепенно у учащихся развивается устойчивость психических процессов и формируется умение сознательно, самостоятельно ставить цель и достигать ее.

Для детей в младшем школьном возрасте характерно такое явление, как рефлексия, это значит, умение объективно анализировать собственные действия и поступки с точки зрения их соответствующей цели. У ребенка появляется внутренний план действий – умение планировать и в уме решать поставленные задачи. Также у детей развиваются познавательные способности, а также произвольное внимание, память, воображение (Приложение 5) [25, c .259].

Процесс обучения – сложная динамическая система, которая осуществляется при взаимосвязанной деятельности учителя и ученика.

Задача учителя состоит не только в том, чтобы давать знания, но и управлять процессом освоения знаний. Задача ученика – овладевать знаниями, способами их приобретения, переработки, сохранения и применения, воспитывая в себе необходимые качества личности.

Основной структурной единицей процесса мышления является действие. Действие – это единица анализа деятельности учащегося.

«Действие, которое выполняется человеком, всегда направлено на какой-то предмет. Предметом действия являются слова, явления, понятия. Действие всегда имеет цель. Действие направленно на результат. Цель действия связана с мотивом. Мотив является важным компонентом действия, он неразрывно связан с целью. Мотив побуждает человека ставить и достигать разные цели, побуждает выполнять соответствующие действия. Ученик каждый день выполняет много учебных действий. Но не всегда он видит необходимость выполнения этих действий. Поэтому часто учебная деятельность для такого ученика становится тяжелой, он не видит в ней никакого смысла» [21, c .254].

Особенно эффективным является обучение, которое начинается с формирования материализованной формы, т е тогда обучение направлено на теоретические знания. Потом вначале необходимо переходить к этапу материального действия, то есть анализировать реальные предметы. На третьем этапе вводится речь, ученики должны комментировать выполненное действие.

Все операции, составляющие данное действие, должны быть усвоены в речевой форме. Сначала действие проговаривается «своими словами», потом постепенно переходят к научной речи, которая выступает конечным результатом этого этапа. Формирование действия во внутренней речи («про себя»), является переходной ступенью для перевода действия в умственный план. На этом этапе действие начинает сокращаться и автоматизироваться [20, c .205].

Можно рассмотреть формирование вычислительного приема 42 – 12 на основе применения теории поэтапного формирования умственных действий.

«Вначале создается проблемная ситуация при решении задачи.

У мальчика было 42 р., 12 р. он потратил. Сколько рублей осталось у мальчика?

Решая с учащимися такую задачу, приходим к выводу, что вычитание вида 42 – 12, еще не умеет выполнять.

Используя палочки или ленты бумаги с кружочками, каждый ученик выполняет практическую работу под руководством учителя.

• Положите на парту 42 палочки. Сколько в этом числе десятков? Единиц?

• Необходимо отнять 12 палочек. Сколько десятков, единиц необходимо забрать? Сколько палочек осталось? Какое это число?» [28, c.31]

То есть каждый ученик, практически выполнил все операции алгоритма, наглядно увидел правило: десятки отнимаются от десятков, единицы от единиц.

В общем, предмет выступает перед ребенком как последовательность конкретных явлений. Объяснение учителем каждого из них, объединение готового алгоритма действий приводит к его механическому запоминанию и как результат поверхностного понимания свойств изучаемых явлений – перенос этого алгоритма на подобные по внешним признакам понятия.

Необходимым условием обучения вычислениям является внимание. Выполнение вычислений требует организации внимания учащихся, потому что из-за невнимательности учащиеся допускают много ошибок.

Внимание – это целенаправленность и сосредоточенность сознания, которое предусматривает повышение уровня сенсорной, интеллектуальной или двигательной активности человека. При организации учебно-воспитательного процесса необходимо учитывать все виды внимания.

Психологи выделяют три вида внимания:

1. «Для привлечения внимания нужен какой-то сильный, резкий внезапный раздражитель. Внимание, которое притягивается силой, необычностью раздражителя, носит название непроизвольное. Для младшего школьника наиболее целесообразным является формирование непроизвольного внимания, этого можно добиться, используя разнообразный познавательный материал, эмоциональность.

2. Сосредоточенность на чем-либо может быть достигнута усилием воли. Сосредоточенность нужна, когда приходится преодолевать какие-то трудности, для того, чтобы быть внимательным для чего-то нужного. Это произвольное внимание. Это самая тяжелая разновидность внимания для маленьких детей, особенно для первоклассников, потому что требует большого волевого напряжения. Произвольное внимание очень важно для младшего школьника. Оно еще нестойкое, дети еще не умеют внутренних способов саморегулирования» [18, c .240].

При выполнении простых, но однотипных заданий младшие школьники отвлекаются чаще. Чем при решении более сложных заданий, поэтому необходимо использовать разные способы и приемы работы. Учителю необходимо так организовать разные виды учебной деятельности, чтобы дети приучались к одновременному контролю за несколькими действиями.

П.Я. Гальперин видит внимание как особенное психическое действие контроля. «Невнимательность школьников связана с неполной сформированностью функции контроля в таких условиях, когда она складывается стихийно» [22, c .312].

«Еще одним источником внимания является интерес, то есть отношение человека к какому-нибудь предмету, к своей деятельности, к поставленной задаче, который выражается в желании узнать что-то новое, раскрыть явление глубже и шире.

Это внимание еще можно назвать мимолетным, но «второстепенным». В этом случае используется термин «после произвольное внимание».

Произвольное внимание не характерно для младших школьников. Для них характерно первичное и вторичное – непроизвольное внимание.

Важным является поддержание внимания детей на протяжении всего урока, придерживаться таких условий организации учебной деятельности:

• удачный темп урока и продуманная его организация;

• четкость, доступность, краткость объяснения;

• опора на активную умственную деятельность детей;

• смена видов и форм работы;

• включение в деятельность всех учащихся» [11, c .302].

У младших школьников внимание характеризуется такими качествами как концентрация, объем, распределение, стойкость.

Концентрация внимания характеризуется сосредоточенностью человека и определяется силой нового раздражителя, которая необходима для погашения бывшей доминанты и создания новой.

Концентрации внимания учащихся можно добиться с помощью выделения основного материала, определенных слов-указаний: запоминай, вспомни и др.

Объем внимания – это объекты, которые человек может одновременно усвоить с одинаковым качеством. Объем внимания у младших школьников ограниченный. Основным условием расширения объема внимания является формирование умений группировать, систематизировать, объединять по сути воспринятый материал.

Распределение внимания – возможность одновременно успешно выполнять два и более, разных видов деятельности.

Стойкость – характеристика внимания во времени. Она определяется продолжительностью сохранения внимания.

Знание видов внимания и умение оперировать этими знаниями на практике очень важно для учителя. Это поможет планировать максимально продуктивно для понимания и запоминания уроки, делать их активными и интересными.

В обучении приходится иметь дело еще с двумя формами организации внимания: коллективной и индивидуальной [8, c .96].

Для формирования вычислительных навыков каждого учащегося в отдельности необходимо учитывать все его психологические особенности. Формой индивидуальной организации внимания является использование алгоритмов, карточек-памяток.

«Необходимым условием формирования вычислительных навыков является память. Память — отображение прошлого опыта человека, которое проявляется в запоминании и дальнейшем припоминании того, что оно воспринял, почувствовал и о чем думал.

Память в младшем школьном возрасте под влиянием обучения развивается по двум направлениям:

• усиление значения словесно–логического запоминания;

• возможность сознательно руководить своей памятью и регулировать ее проявления.

Процессы памяти:

• запоминание – это закрепление тех образов и выражений, которые создаются под впечатлением предметов и явлений действительности в процессе ощущения и восприятия;

• сохранение – это удержание изученного материала в памяти;

• воспроизведение – это процесс проявления представлений памяти, ранее воспринятых мыслей;

• припоминание – наиболее активное воспроизведение, связанное с напряжением и требующее определённых волевых усилий» [4, c .114].

«Важную роль в процессе запоминания играет мотивация. У младших школьников более развита наглядно-образная память, они быстрее запоминают и крепче сохраняют в памяти конкретные сообщения, события, предметы, чем определения и объяснения. Младшие школьники склонны к механическому запоминанию, путем простого преобразования, без осознания существенных связей в пределах запоминаемого материала. Они часто заучивают и воссоздают учебный материал без существенного преобразования. Школьники еще не умеют организовывать содержательного запоминания. Они не умеют разбивать материал на существенные группы, пользоваться логическими схемами, выделять опорные пункты для запоминания.

Чтобы развить память нужно заинтересовать материалом. В начале, запоминается то, что является важным. Очень важным в процессе развития памяти является позитивное отношение к изучаемому материалу.

Школьникам начальных классов присущи такие виды памяти:

• • механическая — основанная на повторении материала без его осознания;

  • оперативная — вид памяти, который возникает в процессе выполнения определенной деятельности;

  • непроизвольная — запоминание без специальной установки;

  • произвольная, которая основывается на специальной установке» [3, c .118].

Основой формирования вычислительных навыков является развитие всех видов памяти и учитель должен это учитывать.

Мышление – процесс обобщенного познания окружающего мира; заключается в установке закономерных связей и отношений.

Умственная деятельность совершается с помощью умственных операций: сравнения, анализа и синтеза, абстракции, обобщения и конкретизации и др.

Различают различные качества мышления. Наиболее существенные из них: самостоятельность, широта, глубина, скорость и критичность ума.

Самостоятельность мышления – это умение человека выдвигать новые задачи и находить необходимые решения и ответы, не обращаясь за помощью к другим. Учитель постоянно в работе встречается с самостоятельностью и несамостоятельностью учеников.

Широта мышления выражается в познавательной деятельности, которая объединяет разные области деятельности.

Глубина мышления – умение проникать в суть вопросов, видеть проблему там, где у других людей вопросов не возникает. Очень важно в глубине мышления стремление к знаниям.

Гибкость мышления выражается в умении быстро переключаться от одного способа решения задачи на другой.

Скорость мышления – это способность человека быстро разбираться в сложных ситуациях, быстро продумать и принять решение [19, c .32].

Способность мыслить постоянно формируется в процессе развития ребенка, развития его познавательной деятельности.

Можно выделить три уровня скорости устных вычислений:

1. Высокий: ученик выполняет одну простейшую математическую операцию не более чем за 4,5 секунды.

2. Средний: ученик выполняет одну простейшую математическую операцию от 4,5 до 6 секунд.

3. Низкий: ученик выполняет одну простейшую математическую операцию более чем 6 секунд [29, c .108].

Формировать у учеников способность к активному и самостоятельному мышлению – наиболее важная задача учителя. Очень важно развивать внимание и память, с учетом индивидуальных особенностей учащегося. На уроках обязательна наглядность и доступность объяснения материала. Необходимо задействовать все виды памяти (зрительная, слуховая), следить за усвояемостью материала и пониманием изучаемого. Следовательно, данные знания о памяти, мышлении, внимании являются обязательными в работе учителя.

В работе учителя есть определенные принципы. Самый важный из них, что работа в классе осуществляется всеми учениками, а не учителем или наиболее успевающими учениками. То есть каждый ученик должен чувствовать себя участником учебного процесса. Важная задача учителя заключается не в доказательстве незнания или слабого знания ученика, а в помощи ребенку осознать, что он может учиться лучше, что у него все получится. Такие действия мотивируют, помогают поверить в собственные силы.

Основные типы заданий:

1. Задания с использованием сравнений .

Очень продуктивным, при формировании вычислительных навыков, является метод наблюдений. При наблюдении учащиеся сравнивают, анализируют, делают выводы. Полученные так знания являются более осознанными и тем самым лучше усваиваются.

Можно рассмотреть, в качестве примера, как изменение суммы в зависимости от изменения одного из слагаемых. В основе здесь лежит прием сравнения.

Задание 1. Решите примеры и сравните их:

2 + 1, 2 + 2.

Необходимо обращать внимание учеников на то, что в одном и в другом примере стоит знак «+», а первые слагаемые одинаковы. Эти примеры схожи. Ищем различия: в первом примере второе слагаемое равно 1, во втором 2, сумма в первом примере равна 3, а во втором – 4.

Ученики отмечают, что во втором примере прибавляем большее, поэтому и получаем большую сумму.

Задание 2. На доске записаны примеры:5 + 3, 4 + 3, 8 – 3, 6 + 3, 7 – 3, 9 – 3

Нужно угадать сходство или различие выражений. Ученики обычно видят, знак действия, затем обращают внимание на то, что в первой группе прибавляется число 3, а во второй – вычитается число 3. Затем педагог задает вопрос: «Что произойдет с ответами примеров в первой группе и во второй? Почему ответы в первой группе больше, чем ответы во второй?»

Задание 3. Что вы замечаете в данных примерах?

1 + 2, 2 + 2, 3 + 2, 4 + 2, 6 + 2, 7 + 2

Ученики видят, что во всех примерах знак «+» и второе слагаемое равно 2, но и то, что последовательность 1, 2, 3, 4 … нарушена и пропущен пример 5 + 2.

Таким образом, мы развиваем математическую наблюдательность, их умение видеть сходства и различия, выявлять определенные закономерности. Дети начинают понимать смысл слова «сравнить».

Так же могут предлагаться задания с ошибками, которые требуют исправления.

Задание 4. Найди ошибку. Также могут предлагаться задания, у которых уже дан знак отношения и одно из выражений, а другое выражение надо составить или дополнить: 8

• (10 + 2)=8

— 10 + … Выражения могут быть с разными действиями. Главная цель таких заданий – усвоить теоретические знания об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Они помогают в выработке вычислительных навыков [12, c.43] .

2. Задания на классификацию и систематизацию знаний .

Главное в заданиях на классификацию — умение выделять признаки предметов и устанавливать между ними сходство и различие. Известно, что при разбиении множества на классы необходимы следующие условия:

1) ни одно из подмножеств не пусто;

2) подмножества попарно не пересекаются;

3) объединение всех подмножеств составляет данное множество.

При выполнении таких заданий необходимо учитывать данные условия.

3. Задания на выявление общего и различного .

Основная характеристика данных заданий это выделение существенных признаков математических объектов, их свойств и отношений. Благодаря им ученики сами находят математические свойства и правила, которые в математике строго доказываются.

Задание 1. Необходимо рассмотреть рисунок и быстро посчитать окна (Приложение 7).

Дети могут предложить следующие способы: 3+3+3+3, 4+4+4 или 3*4=12; 4*3=12.

Затем сравниваем полученные равенства, Находим что общего, а в чем различие. Отмечается, что оба произведения одинаковые, а множители переставлены. Таким образом, делаем вывод — если множители переставить, то произведение не изменится или от перестановки множителей значение произведения не изменится.

4. Задания с многовариантными решениями .

Многовариантные задания — это система упражнений, благодаря которым можно усвоить правило, выработать необходимый вычислительный навык на его основе.

Задание 1. Записать число 50 тремя одинаковыми цифрами и знаками действий. Найти несколько разных решений.

Задание 2. Какое число надо прибавить к 35, чтобы получить круглое?

5. Задания с элементами занимательности .

Они направлены на закрепление вычислительных навыков. Факт занимательности заинтересовывает детей, они стремятся выполнить все действия правильно и посмотреть к чему это приведет.

Пример этих заданий «Магические или занимательные квадраты» Решение квадратов интересно для школьников всех возрастов.

6. Задания на нахождение значений математических выражений .

Дано математическое выражение и необходимо найти решение. Эти задания имеют много вариантов. Можно предлагать числовые математические выражения и буквенные, например:

— найти разность чисел 150 и 10.

— найдите значение выражения С – К, если С = 150, К = 10.

Выражения вслух можно озвучить по-разному: из 150 – 10; 150 минус 10; уменьшаемое 150, вычитаемое 10; найти разность чисел 150 и 10; уменьшить 150 на 10 и т.д.

Можно дать выражения с ошибками, которые детям предстоит найти: Задание 1. Найди ошибки в выражениях (Приложение 8).

Также можно выполнить задание в таблице (Приложение 9).

Главная задача на нахождение значений выражений – выработать твердые вычислительные навыки.

7. Комбинаторные задачи .

Комбинаторика – это раздел современной математики.

Они развивают мышление детей, воспитывают у них умения применять полученные знания в различных ситуациях посредством выработки навыков и повторения. Выполнение разбиения множеств, составление комбинации по определенным признакам и классификация лежит в основе многих сфер человеческой деятельности.

Задание 1. Если умножить два одинаковых числа, получится 25

Чему были равны множители? Найди разные решения.

Задание 2. На складе было 9 полных бочонков меда, 9наполовину заполненных медом и 9 пустых бочонков. Как распределить все бочонки между тремя покупателями так, чтобы каждый получил одинаковое количество меда и бочонков (мед не нужно перекладывать из одного бочонка в другой).

Использование разнообразных заданий приводит к интересу у детей, стимулирует их к активную деятельность и позволяет более прочно сформировать вычислительные навыки. Примеры карточек по обучению вычислительных навыков приведены в Приложении 10 [40, c . 81-85].

Современная педагогика требует от учителей использование большой методологической базой. Педагог должен пользоваться разнообразными методами начиная от устного объяснения до презентаций. Разнообразие при преподавании новой темы (презентации, беседы, диспуты…) помогают детям быстрее понять и усвоить материал. В начальной школе детям сложно сосредоточиться на новой информации. Поэтому учителю нужно использовать все новые и новые методы, лучше в игровой форме обучения, чтобы заинтересовывать детей с разным уровнем интеллектуального развития. Даже опрос домашнего задания можно проводить в игровой форме. Для этого, например, подойдут карточки с задачами, которые следует раздавать нескольким ученикам. Карточная система опроса помогает экономить время на контроле домашнего задания и покажет те темы, которые вызывают у детей наибольшие проблемы в усвоении. В отличие от других предметов, на уроках математики проводить беседы между учениками довольно сложно, но игнорировать такую методику нельзя. Беседы помогают детям лучше усвоить новую тему.

Современный урок математики в начальной школе также должен учить ребенка грамотно рассуждать, приводя аргументы по той или иной конкретной цели. Для этого учитель, например, на доске напишет несколько примеров с неправильным решением. Дети должны найти ошибки, привести аргументы, почему написанное значение неправильно, и как верно. Этот метод помогает детям применить заученные правила и лучше их понять.

Педагог должен планировать заранее урок, подбирать доступные именно для этого класса задания. Важно не ориентироваться только на сильных или только на слабых учениках. Смысл дифференцированного подхода в том, что каждый учащийся получает именно то количество информации, которое ему необходимо. Для того, чтобы помочь слабым и развивать сильных педагог должен готовить индивидуальные задания. Если пользоваться различными методами, планировать тщательно каждый урок, то педагог обязательно добьётся результатов. Пользуясь современными рекомендациями к организации учебного процесса, педагог обязательно преуспеет, организовав грамотную индивидуальную работу.

Итак, индивидуальный подход в процессе обучения очень важен. Он даёт возможность увидеть и исправить пробелы в знаниях, воспитать в каждом ученике желание учиться. Каждый ребёнок – это личность, и индивидуальный подход предусматривает общение с каждым именно, как с личностью. Есть дети, успевающие в знаниях и понимающие сразу объяснения учителя, есть те, которым приходится объяснить, применяя дополнительный материал, наглядный.

Важна и дифференциация в обучении, она позволяет сформировать у учеников чувство ответственности перед товарищами за результат совместной работы и при этом, дает возможность научиться самостоятельно принимать решения и отстаивать их правильность, а также приучает прислушиваться к мнению товарищей и вовремя исправлять допущенные ошибки. Поэтому дифференциация способствует формированию у детей самоконтроля и правильной самооценки.

В обучающем процессе важно знать детскую психологию. Учитель должен научить ставить цели, планировать, развивать познавательные способности, внимание, память, воображение.

Задача учителя не только давать знания, но и управлять процессом освоения знаний. Педагог должен пользоваться такими понятиями, как мышление, эмоциональность, сосредоточенность, интерес. Знать психологические процессы необходимо не только для того, чтобы давать доступный по возрасту материал, правильно его преподносить и закреплять, но и для развития личности ребенка.

2.1. Организация исследования по формированию вычислительных навыков и умений младших школьников

Исследование работы проводилось на базе Муниципального бюджетного общеобразовательного учреждения Зуйская средняя школа №1 им. А. А. Вильямсона Белогорского района. Организация практической работы по формированию вычислительных навыков и умений младших школьников строилась с учетом нижеизложенных данных.

В 1-А классе 23 учащихся, в 1-Б классе 22 учащихся.

Для диагностики уровня успеваемости использовался анализ процесса освоения новых знаний и выполнения классных, самостоятельных и домашних работ.

В качестве диагностических критериев использовались следующие знания и умения учеников по предмету математика в первом классе:

1. Моделировать расположение предметов на плоскости (справа, слева, сверху, снизу) и в пространстве (сзади, спереди).

2. Упорядочивать события по времени (раньше, позже, ещё позднее, сейчас).

3. Уверенно разбираться в направлении движений (направо, налево, вперёд, назад).

4. Сравнивать предметы по количеству (больше, меньше, равно), давать количественное сравнение – на сколько больше, на сколько меньше.

5. Знать названия и четко называть последовательность чисел от 1 до 20.

6. Распознавать геометрические фигуры: точка, кривая, прямая, ломанная, отрезок, а также круг, треугольник, прямоугольник, квадрат, многоугольник. Чертить эти геометрические фигуры, используя линейку (за исключением окружности).

7. Писать прописью числа от 1 до 10 и соотносить графическую запись и прописную.

8. Применять и понимать действия и знаки: плюс, минус, равно.

9. Уверенно различать и знать названия основных цветов.

10. Классифицировать группу предметов по основным признакам (цвет, форма, материал, размер).

11. Знать и уметь употреблять термины: цифра, число, однозначное число, двузначное число.

12. Уметь увеличивать или уменьшать число на 1.

13. Знать единицу длины – сантиметр и уметь измерять длину отрезка с помощью линейки [53, c .25].

Результаты эксперимента представлены на рис.2.1.

Рисунок 2.1. – Успеваемость учащихся на констатирующем этапе эксперимента

Как видно из диаграммы, на констатирующем этапе эксперимента степень освоения знаний в двух группах была примерно равна. Детей с высокой степенью освоения знаний было по пять человек в каждой группе, с низкой 3 в экспериментальной группе и 4 в контрольной, что составило 13 и 18% соответственно, со средней 15 детей в первой группе (65%) и 13 во второй (59%).

Анализ ошибок при выполнении контрольных работ проводился по следующим категориям:

Категория 1 – ошибки в арифметических действиях и вычислениях ( 71 %);

Категория 2 – ошибки в определении знаков неравенств или заполнении пропусков и подчеркивании сумм ( 47%) ;

Категория 3 – ошибки в ходе черчения отрезков и сравнения их длин ( 41%) ;

Категория 4 – ошибки в записях числа в порядке возрастания (убывания) или на порядок выполнения арифметических действий ( 29%) .

Полученные результаты говорят о том, что вычислительные умения и навыки первоклассников еще не сформированы, и этому вопросу надо уделять серьезное внимание.

Учитывая результаты констатирующего этапа, на формирующем этапе эксперимента использовалось 3 вида форм работы: фронтальная, индивидуальная и групповая.

Фронтальная работа была необходима в связи с едиными учебными программами, развитием индивидуальных способностей. При фронтальной работе выяснилось, что ученик проявляет себя как личность, демонстрирует свои знания, эрудицию, память, желание и умение трудиться в коллективе. Учитель при этом, пользуется общими для всех задачами, в процессе может наблюдать и оценивать общий настрой, отношение к материалу и друг другу.

Особенно интересны приёмы занимательности с элементами удивительного и неожиданного. Например, на уроках использовалось «Математическое лото». В конверте были подготовлены карточки – большая и маленькая. Маленькие с упражнениями, их больше, а большие с ответами. Школьник достает из конверта карточку, решает пример и накрывает ею соответствующий ответ. Карточки кладут лицевой стороной вниз.

Если все примеры решены правильно, то обратные стороны наложенных карточек составляют задуманный рисунок. Проходя между рядами, легко можно было оценить результат работы ребенка. Так как это занимательное задание и в какой-то мере оформленное в форме игры, то даже слабые ученики старались с ним справиться.

Также использовалось два вида следующих игр: игровая ситуация, где интересна форма задания, и математическая игра с интересным содержанием. Можно сочетать эти два вида. Например, игра “Куча мала”. «Ученикам предлагается запомнить сначала 3, а затем 5, 6, 7 чисел. Учитель называет числа один раз, а ученики записывают их. После знакомства с таблицей сложения ученики складывают последовательно каждые два числа» [14, c .301].

На уроках применялись интерактивные презентации. Презентации с элементами игры в основном использовались на уроках закрепления и обобщения знаний, а также в качестве разминки в начале урока открытия новых знаний.

Еще использовались на уроках отработки знаний и навыков: в игровой форме детям гораздо проще и интереснее выполнять однотипные задания. На практике мы увидели, что через дидактическую или математическую игру, реализованную на различном учебном материале, формируются не только вычислительные навыки, но и повышается интерес к изучению нового материала.

Также использовались учебные задания с нематематической информацией, что привносило разнообразие в процесс обучения вычислительным навыкам. Форма их записи самая разнообразная: цепочки примеров, простые и с разветвлением, таблицы, магические квадраты, блок-схемы – простые, с условием без цикла и с циклом. В предлагаемых заданиях даны словесные формулировки познавательных вопросов, возможные ответы, из которых один правильный, математические задания вычислительного характера для проверки выбора ответа и информация о животных или событиях (ение 11) [15, c .164].

В ходе исследования были обнаружено, что дополнительные сведения на уроке не загружают детей, а лишь способствуют усвоению программного материала за счёт создания интереса к учению и повышению познавательной активности. Детям необходима смена деятельности для расширения кругозора, побуждения узнавать новое. Развитие стремления узнать новое – одна из воспитательных целей этих заданий.

В этих играх важно, что они представляют собой систему, следовательно, меньше времени затрачивается на объяснение нового материала. Игры постепенно усложнялись, но интерес к ним не пропадал. Играми заметно ускорялась скорость решения математических заданий, что важно, не под давлением «нужно знать и иметь», а автоматически, под действием игр.

В качестве одного из средств формирования вычислительной культуры младших школьников можно рассматривать текстовые задачи ( 12).

В условиях этих задачах могут использоваться реальные примеры из жизни, что объясняет детям необходимость изучения вычислительных навыков [21, c .254].

Очень активно в практической части исследований использовалась индивидуальная форма работы. Индивидуальная форма работы дает оптимальную занятость учащихся. В последнее время очень важную роль играет самостоятельная работа, которая может носить творческий характер. Необходимо на уроке использовать задания для самостоятельной деятельности творческого характера, которые нацелены на формирование у младших школьников вычислительных навыков, так они способствуют усвоению знаний. При этом каждый ученик получает свое задание, которое он выполняет независимо от других. Чаще всего это задания–карточки, где учитель имеет возможность подобрать их индивидуально каждому ученику, в зависимости от успеваемости (Приложение 10).

В исследовании было замечено, что индивидуальные задания особенно важны для школьников с негативным отношением к учебе. Даются посильные задания. Такого рода задания требуют выполнения различных преобразований и обобщений с опорой на ранее приобретённые знания и умения. Знания углубляются, становятся более совершенными, а мышление учащихся достигает уровня продуктивной деятельности (Приложение 13).

В карточке может быть несколько заданий с разными уровнями. Ученик решает доступное и переходит к следующему, это хорошо диагностирует уровень подготовки ученика [42, c .325].

Как показывает практика, использование таких заданий способствует эффективной организации самостоятельной деятельности младших школьников, а также повышает эффективность процесса формирования соответствующего вычислительного навыка.

Большую роль на уроках математики играют тесты. Тесты обладают целым рядом положительных характеристик:

• Быстрота проверки выполненной работы,

• Оценка достаточно большого количества учащихся,

• Возможности проверки усвоения теоретического материала,

• Проверка большого объёма материала малыми порциями,

• Объективность оценки результатов выполненной работы.

В работе учителя начальных классов тесты выполняют пропедевтическую функцию. Самые доступные тесты в младшем школьном возрасте с одним ответом (Приложение 14) [52, c .27].

Тесты составлялись с учетом самых частых ошибок, что позволяло их исправлять ученикам и запоминать правильный вариант решения. Сочетание индивидуальных заданий должно быть разумным. Это способствует развитию математической культуры и влияет на самообразование и саморазвитие младших школьников.

Применялась и групповая форма работы. При групповой работе класс временно делили на группы, которые создавали по мере необходимости (по 4 чел., 2 чел., 6 чел.).

В группе важно чтобы были дети с разной успеваемостью, что даёт возможность сильным помогать слабым, а слабым – тянуться за сильными. Контактируя в группе, учащиеся начинают лучше понимать друг друга, давать объективную оценку знаниям, умениям и поступкам друг друга. Выбирается ученик – консультант, руководящий ходом работы в каждой группе. Учащиеся работают по заданию, консультант следит за работой, в случае необходимости руководит. Ответы на групповые задания даются поочередно. Оценивается работа всей группы (Приложение 15) [49, c .40].

Упражнения – это лишь начальное звено в формировании умения работать в группах. Работа в группах учит совместной работе учеников, влияет на активацию мыслительной деятельности. Ученики более раскрепощены, менее боятся таких заданий. Школьники в процессе общения обсуждают полученные результаты, подводят итоги, оказывают помощь друг другу в поиске ошибок. Всё это превращает учение не только в усвоение готовых знаний, но и в процесс познания. Групповая форма учебной работы позволяет учитывать особенности и запросы школьников.

Коллективная форма организации обучения – это один из способов развития индивидуальности и творческой активности учащихся. Эта форма также хорошо влияет на формирование вычислительных навыков. Учеников делили на постоянные пары. Задание читают друг другу, затем отвечают. Каждый из пары получает противоположное задание. После работы в постоянных парах начинается работа в парах сменного состава.

Игра «Ручеёк» способствует отработке навыков устных вычислений, активизирует деятельность учащихся, развивает произвольное внимание и любознательность. Игра «Ручеёк»: задание у каждого индивидуальное. Ребята сидят в ряду. Затем один вариант начинает движение: с первой парты ученик идёт на последнюю, а остальные передвигаются на одну парту вперёд. Движение идёт до тех пор, пока все ученики следующего варианта не займут свои места. Можно поменять вариант первого ряда с вариантом второго ряда и т.д. [46].

2.2. Анализ полученных результатов и рекомендации учителям по рациональному использованию индивидуальных и групповых методов в обучении математике в начальной школе

Применение различных форм работ в исследовании привели к положительным результатам. Получилось быстро диагностировать уровень знаний каждого ученика, что позволило более продуктивно подбирать индивидуальные задания, исправлять пробелы в знаниях. Коллективные и групповые формы помогли детям сблизиться друг и другом, почувствовать уверенность в своих силах. Детям очень интересны уроки в игровой форме, что приводит к быстрому пониманию и запоминанию нового материала и закреплению старого. Вариативность всех форм обучения помогла детям в максимально возможно изучить вычислительные навыки, в соответствии с программой.

Разработанная система упражнений и заданий даёт возможность каждому ребёнку проявить активность в поисковой работе, активизирует мыслительную деятельность, умение находить закономерности и особенности в решении различных видов примеров. Разнообразные задания позволяют развивать гибкость мышления, возможность находить свой способ решения, развивать математическую речь ребёнка, не вызывает эмоциональной усталости и монотонности в работе. Вместе с тем количество упражнений и заданий достаточно для формирования прочных вычислительных умений и навыков.

Целенаправленная и системная работа позволяет сформировать высокий уровень вычислительных умений и навыков обучающихся.

Очень интересно было диагностировать у ребят психолого-педагогические проблемы. Ведь у каждого ребенка индивидуально мышление, память, восприятие нового материала. Без этих знаний невозможен индивидуальный подход к ученикам. Одни быстро понимают, другим нужно объяснять понятней, одни запоминают сразу, другим нужно учить и постоянно повторять, одни быстро ориентируются в задании, другим нужно подумать какое-то время. На развитие памяти и мышления детям давались различные задания. Во-первых, по ним можно было определить уровень развитие мышления, во-вторых, развить психологические качества.

На формирующем этапе в первой четверти была проведена проверочная работа.

1. Какая цифра стоит после цифры 2?

2. Нарисуй 3 кружочка.

3. Выдели верные примеры.

4. Сколько треугольников на рисунке?

5. Поставь правильно знак: больше, меньше, равно.

6. Реши примеры.

Во второй четверти следующая контрольная работа (один вариант):

1. Заполни пропуски … цифрами.

10 , 9 , … , … , 6 , … , 4.

2. Реши примеры.

3. Реши задачу.

На заборе сидели четыре котёнка. Два котёнка убежали. Сколько котят осталось сидеть на заборе?

4. Поставь правильно знак: плюс или минус.

5. Поставь правильно знак: больше, меньше, равно.

Контрольная работа в третьей четверти (один вариант)

1. Реши задачу.

Маша съела 3 конфеты, а потом ещё 3 карамельки. Сколько всего конфет съела Маша?

2. Реши примеры.

3. Реши задачу.

Начерти 2 отрезка. Длина одного отрезка равна 4 см, а длина второго отрезка на 3 см длиннее.

4. Поставь правильно знак: плюс или минус.

5. Поставь вместо пропуска … цифру, чтобы равенство стало верным.

Из контрольных работ видно, как изучался и усложнялся учебный материал.

Если рассматривать оценивание знаний через призму индивидуальности учащегося, то конечно, безбальная система намного приоритетней традиционной «пятибалльной».

Здесь необходимо рассмотреть приемы формирования вычислительных навыков.

«Приемы, теоретическая основа которых – конкретный смысл арифметических действий. К ним относятся:

а+2, а+3, а+4, а+0;

• табличное сложение и вычитание с переходом через десяток в пределах 20;

• нахождение табличных результатов умножения, прием нахождения табличных результатов деления и деления с остатком, прием умножения единицы и нуля» [52, c .31].

«Это первые приемы вычислений, которые вводятся сразу после ознакомления учащихся с конкретным смыслом арифметических действий. Они, собственно, и дают возможность усвоить конкретный смысл арифметических действий, поскольку требуют применения конкретного смысла.

1. Приемы теоретической, основой которых служат свойства арифметических действий. К этой группе отнесем большинство вычислительных приемов:

• сложение и вычитание для случаев вида 53 ± 20, 47 ± 3, 30 – 6, 9 + 3, 12 – 3, 35 ± 7, 40 ± 23, 57 ± 32, 64 ± 18;

• аналогичные приемы для случаев сложения и вычитания чисел больших, чем 100, а также приемы письменного сложения и вычитания;

• умножение и деление для случаев вида 14 × 5, 5 × 14, 81 : 3, 18 × 40, 180 : 20, аналогичные приемы умножения и деления для чисел больших 100 и приемы письменного умножения и деления.

Общая схема введения этих приемов одинакова: сначала изучаются соответствующие свойства, а затем на их основе вводятся приемы вычислений.

2. Приемы, теоретическая основа которых являются связи между компонентами и результатами арифметических действий. К ним относятся приемы для случаев вида 9 × 7, 21 : 3, 60 : 20, 54 : 18, 9 : 1, 0 : 6. При введении этих приемов сначала рассматриваются связи между компонентами и результатом соответствующего арифметического действия, затем на этой основе применяется вычислительный прием.

3. Приемы, теоретическая основа которых – изменение результатов арифметических действий в зависимости от изменения одного из компонентов. Это приемы округления при выполнении сложения и вычитания чисел (45 + 18, 511 – 297) и приемы умножения и деления на 5, 25, 50. Для введения этих приемов также требует предварительного изучения соответствующих зависимостей.

4. Приемы, теоретическая основа которых — вопросы нумерации чисел. Это приемы для случаев вида а ± 1, 10 + 7, 17 – 10, 17 – 7, 67 × 10, 1300 : 100; также аналогичные приемы для больших чисел. Введение этих приемов предусматривается после изучения соответствующих вопросов нумерации (натуральной последовательности, десятичного состава чисел, позиционного принципа записи чисел).

5. Приемы, теоретическая основа которых — правила. К ним относятся приемы для двух конкретных случаев: а × 1, а × 0. Поскольку правила умножения чисел на единицу и нуль есть следствия из определения действия умножения целых неотрицательных чисел, то они просто сообщаются учащимся и в соответствии с ними выполняются вычисления» [42, c .325].

Этапы формирования вычислительных навыков.

«1. Вначале идет подготовка к новому приёму.

Здесь ученик готовится к усвоению вычислительного приёма, а именно освоить теоретическую базу приема. Например, принято считать, что ученики подготовлены к восприятию вычислительного приёма ±2, если они ознакомлены с конкретным смыслом действий сложения и вычитания, знают состав числа 2 и овладели вычислительными навыками сложения и вычитания вида ± 1.

2. Знакомство с вычислительным приёмом.

Здесь усваивается сама суть приёма: что выполнять, в каком порядке и почему именно так. На этом этапе важна наглядность. Например, прибавляя к 7 число 2, придвигаем к 7 кубам 2 куба по одному.

В других случаях в качестве наглядности логично использовать развернутую запись. Например, при введении приёма внетабличного умножения выполняется запись:

14 × 2=(10 + 4) × 2=10 × 2 + 4 × 2 = 20 + 8 = 28

Важно, особенно на первых парах, каждое действие проговаривать вслух.

Вначале учитель объясняет и помогает учащимся, затем они выполняют задания самостоятельно.

3. Следующий этап – закрепление знаний и выработка вычислительного навыка.

Здесь учащиеся усваивают материал и начинают самостоятельно, быстро вычислять, т е вырабатывать навык» [39, c .71].

По Л. В. Занкову «формирование навыков проходит три различных этапа, при этом у учителя может быть два пути – прямой и косвенный.

Прямой путь это когда сообщается учащимся алгоритм выполнения операции, на основании которого школьники многократно ее выполняют. В результате достигается запоминание и вырабатывается навык.

Косвенный путь это, прежде всего, включение учеников в продуктивную творческую деятельность, в самостоятельной поиск алгоритма выполнения операции. Продуктивней, конечно, использовать косвенный путь, а прямым пользоваться только по мере необходимости. В чистом виде этими путями педагог не пользуется» [27, c .424].

Для первого этапа характерно осознание и создание алгоритма выполнения задания. Устные рассуждения переводятся в запись математическими знаками. Отсюда вытекает характерный признак этого этапа — подробная запись выполнения операции, с которой в данный момент работают ученики. Здесь используется в основном косвенный путь. Прямой путь возникает только при условии выполнения промежуточных, знакомых детям операций. Результатом этого этапа является выработка алгоритма выполнения операции и его осознание.

124 × 55 = 124 × (10 + 5) = 124 × 10 + 124 × 5 = 1240 + (100*5) + (20*5) + (4*5) = 1240 + 500 + 100 + 20 = 1860

На втором этапе формируется правильное выполнение операции. Здесь используется выработанный на первом этапе алгоритм действий и умение предвидеть, чему приведет то или иное изменение компонентов операции.

Используются оба пути, однако косвенный путь продолжает быть ведущим, прямой же используется в качестве второстепенного. Ученикам даются такие задания, которые ставят детей в позицию активного творческого поиска, где они используют свои знания в нестандартном преобразованном виде.

Например, даем задание: изменить в произведении 284 × 25 одну цифру так, чтобы значение произведения стало пятизначным числом.

В результате найденных преобразований каждый ученик получает от 6 – до 12 произведений, изменяя цифру во втором или в первом множителе:

284 × 35, 284 × 45, 284 × 55, 284 × 65, 284 × 75 (85, 95, 55)

384 × 25, 484 × 25 (584, 684, 784, 884,984) × 25.

От учащихся не требуется нахождения и составления всех возможных решений. После объединения всех случаев, которые нашли разные ученики, анализируем, находим с ними определенную закономерность, отыскиваем пропущенные варианты [10, c .56].

В таких заданиях важным является индивидуализация, т е нет жестких установок на решение этого задания, а только рекомендации «Постарайся найти не одно решение».

Третий этап формирования навыка приводит к наработке высокой скорости выполнения операции. Здесь уже основным является прямой путь. Учитель должен развить интерес и привести к тому, что детям интересно выполнять задания.

Формирование вычислительных умений и навыков – это сложный длительный процесс, он зависит от индивидуальных особенностей ребенка, уровня его подготовки и организации вычислительной деятельности.

На современном этапе развития образования очень важно не только формировать прочные вычислительные умения и навыки, но и всесторонне развивать личность ребенка.

Формирование вычислительных навыков на уроках математики является главным. Важной формой работы по формированию вычислительных навыков являются задания. «Овладение вычислительными навыками имеет большое образовательное, воспитательное и практическое значение:

• образовательное значение: устные вычисления важны для усвоения многих вопросов теории арифметических действий, а также для улучшения понимания письменных приемов;

• воспитательное значение: устные вычисления способствуют развитию мышления, памяти, внимания, речи, наблюдательности и сообразительности;

• практическое значение: в жизни необходима правильность вычислений, и важно тогда, когда письменно решить нет возможности» [15, c .124].

2.3. Методические рекомендации для педагогов по формированию вычислительных навыков и умений младших школьников

Начинающим педагогам можно выдать следующие рекомендации.

Педагогу на уроке необходимо быть собранным, четко и ясно ставить задачи перед учениками, поэтапно вести детей к запланированной цели. Быть доброжелательным, не повышать голос, не возмущаться незнанием или непониманием. Понимать, что если многие ученики не знают и не понимают материал, то ошибку надо искать в преподношении нового материала, искать свои ошибки, разбирать и исправлять. Нельзя перебивать учеников, нужно дослушать мысль до конца. Нечеткий ответ может быть следствием неясного вопроса.

Внимательно наблюдать за реакцией учеников на рассказ, задание. Потеря внимания – важный сигнал о необходимости изменить темп, повторить объяснение или использовать дополнительный материал. Не забывать, что показателями внимания могут быть активное слушание, сосредоточенность на задании. Темп урока должен быть интенсивным, но посильным для большинства. Необходимо стимулировать учащихся задавать вопросы.

Организация урока, Проверка ранее усвоенных знаний, Объяснение нового материала, Первоначальное закрепление нового материала, Применение ТСО, наглядных пособий, Культура речи и письма, Затруднения в организации внеклассных мероприятий

Чаще предлагать учащимся современные дидактические игры. Проверка и оценка знаний, умений учащихся по математике. Они оцениваются по результатам устного опроса, текущих и итоговых письменных работ. Усвоение содержания материала проверяется программой по математике для четырехлетней начальной школы.

Усвоение наиболее существенных вопросов учебной программы проверяются итоговой контрольной работой. При проверке определяется осознанность знаний и глубина навыков, а так же умение применять их к решению учебных и практических задач. Как мы уже рассмотрели, в первом классе не используется пятибалльная система.

У младших школьников успехи определяются отношением ученика к учебе, его старательностью при выполнении заданий учителя, умениями, навыками, уровнем усвоения учебного материала. Оценка ребенку в первом классе в основном в виде похвалы. Во всех случаях оценка должна даваться доброжелательным тоном и нести положительные стимулы к дальнейшей работе ученика. Замечания должны содержать аргументы и должны быть доступны для понимания ученику.

Оценивание должно быть с учетом индивидуальных особенностей ученика. Письменную работу в тетрадях нужно проверять по мере выполнения, исправлять ошибки и сразу оценивать. В течение года учитель наблюдает за усвоением материала каждым учеником, отмечая его успехи в индивидуальной карте. На родительском собрании сообщается, какую тему их ребенок усвоил успешно, а над чем надо поработать.

Исследования на констатирующем этапе эксперимента показали недостаточное качество вычислений учащихся. Особенно страдает культура устного счета. В настоящее время в реальной школьной практике возрастает количество детей, которые испытывают трудности в учёбе, требуют особого внимания педагога. Поэтому овладение вычислительными навыками имеет большое образовательное, воспитательное и практическое значение.

Основываясь на проведенных исследованиях, была проведена опытно–экспериментальная работа с учениками первого класса с целью выявления эффективности применения указанных выше методик.

Методики, использованные нами на практике, хорошо зарекомендовали себя в процессе обучения. Повысилась успеваемость школьников, а количество ошибок снизилось в 2 раза. Есть основание полагать, что при постоянном их использовании в учебно-воспитательном процессе, методы индивидуального и групповых подходов будут иметь еще большую эффективность, формируя устойчивый интерес учащихся к изучаемой теме и учебному процессу.

В целом необходимо формировать у учеников способность к активному и самостоятельному мышлению. Очень важно развивать внимание и память с учетом индивидуальных особенностей учащегося. На уроках обязательна наглядность и доступность объяснения материала. Необходимо задействовать все виды памяти (зрительная, моторная, слуховая), следить за усвояемостью материала и пониманием изучаемого.

Формирование вычислительных навыков – одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе, поскольку вычислительные навыки необходимы при изучении арифметических действий.

Школа всегда уделяла большое внимание проблеме формирования прочных и осознанных вычислительных умений и навыков, так как содержательную основу начального математического образования оставляют понятия числа и применения арифметических действий при решении содержательных задач. Программы по математике включают большой интересный материал по проблеме формирования прочных навыков вычислений, однако, по-прежнему некоторые вопросы понимания и отработки навыка арифметических вычислений являются для младших школьников довольно сложными.

Были наиболее полно раскрыть вопросы индивидуального и группового подхода к учащимся. Основываясь на результатах, полученных в ходе проведения экспериментальной работы, нами была разработана система заданий, способствующих совершенствованию вычислительных навыков, а так же направленных на увеличение количества сформированных вычислительных приемов. Эти задания включались в уроки математики на различных этапах их проведения.

Результатом такой работы стало формирование у учащихся экспериментального класса более прочных и осознанных вычислительных навыков. Так же эти задания способствовали увеличению количества сформированных вычислительных приемов.

Таким образом, доказана гипотеза о том, что такие факторы как содержание учебного материала, использование индивидуального подхода при обучении школьников способствует развитию познавательной деятельности учащихся и отработке их вычислительных умений и навыков.

Рассмотрен также важный вопрос оценивания знаний младших школьников и почему это имеет такое большое значение, особенно в современном мире. Разработаны практические рекомендации учителям по формированию вычислительных умений и навыков младших школьников.

Главным выводом работы является подтверждение необходимости применения индивидуального подхода на уроках математики при изучении вычислительных навыков. Важность не просто преподать новый материал, но и преподать его максимально понятно каждому учащемуся. Это ежедневная работа учителя над планированием предстоящего урока и постоянное расширение знаний не только в методах обучения, но и в элементарных знаниях детской психики. Идти в ногу с современным миром.

Система обучения с индивидуальным подходом к учащимся дает возможность каждому ученику встать на путь самосовершенствования, самопознания, развития своих способностей и талантов.

Таким образом, в процессе выполнения работы намеченная программа исследования была выполнена, поставленные задачи решены, цель исследования, состоявшая в определении наиболее эффективных образовательных технологий обучения младших школьников вычислительным умениям и навыкам на уроках математики , достигнута.

1. Актуальные проблемы методики обучения математике в начальных классах / Под ред. М.И. Моро, А.М. Пышкало. — М.: Просвещение, 2005. — 248 с.

2. Аргинская И.И. Математика. Методическое пособие к учебнику 2-го класса четырехлетней начальной школы / И.И. Аргинская. — М.: Центр общего развития, 2000. — 108 с.

3. Бабанский Ю.К. Методы обучения в современной общеобразовательной школе / Ю.К. Бабанский. — М.: Просвещение, 2002. — 118 с.

4. Бабанский Ю.К. Оптимизация учебно-воспитательного процесса / Ю.К. Бабанский. — М.: Просвещение, 2002. — 114 с.

5. Бабанский Ю.К. Проблемное обучение как средство повышения эффективности учения школьников / Ю.К. Бабанский. — Ростов-н/Д., 2004.- 125 с.

6. Бантова М.А, Бельтюкова Г.В.. Методика преподавания математики в начальных классах- М.: Просвещение, 1986.

7. Богоявленский Д.Н. Психология усвоения знаний в школе / Д.Н. Богоявленский, Н.А. Менчинская. — М.: Академия, 2002. — 279 с.

8. Брушлинский А.В. Психология мышления и проблемное обучение / А.В. Брушлинский. — М.: Знание, 2005. — 96 с.

9. Видинеев Н.В. Природа интеллектуальных способностей человека. –М., 1989 . — с. 52

10. Чилингорова Л., Спиридонова Б. Играя, учимся математике. — М.:Просвещение, 1993.

11. Вилькеев Д.В. Познавательная деятельность учащихся при проблемном характере обучения основам наук в школе / Д.В. Вилькеев. — Казань: Айрис-Пресс, 2007. — 302 с.

12. Волина В.. Праздник числа- М.: Знание, 1993.

13. Выгодский Л.С. Собрание сочинений в 6 т. –Т.6 – М. : Просвещение , 1984 . — с. 369

14. Газман О.С. Каникулы: игра, воспитание; М. : Просвещение 2000 . — с.301

15. Гальперин П.Я. Методы обучения и умственное развитие ребенка / П.Я. Гальперин. — М.: Изд-воМГУ, 2001. — 164 с.

16. Гобова Е.С. Зачем ходить в школу?; М. : Просвещение 2002 . — с.236

17. Гуткина Н.И. Психологическая готовность к школе. – М.: Образование, 1996 . — с. 311

18. Давыдов В.В. Проблемы развивающего обучения: Опыт теоретического и экспериментально-психологического исследования. — М.: Педагогика, 2006. — 240 с.

19. Давыдов В.В. Программа развивающего обучения по математике (система Д.Б. Эльконина — В.В. Давыдова).

    I-III классы / В.В. Давыдов, С.Ф. Горбов, Г.Г. Микулина, О.В. Савельева. — М.: МИРОС, 2000. — 32 с.

20. Далингер В.А. Методические системы развивающего обучения математике в начальной школе / В.А. Далингер, Л.П. Борисова. — Омск: Изд-во ОГПУ, 2004. — 205 с.

21. Данилова Л.А. Методы диагностики младших школьников.- М.: Академия, 1997 с. 254

22. Дружинин В.Н. Психология общих способностей. – С-Пб.: Питер, 1999 . — с. 312

23. Житомирский В.Г., ШевринЛ.Н.. Путешествие по стране Геометрии — М.: Педагогика-пресс, 1994.

24. Зак А.З. Развитие интеллектуальных способностей у детей 6-7 л. –М. .: Просвещение ,1996 . — с. 168

25. Зак А.З. Развитие интеллектуальных способностей у детей 8 лет: Учебно-методическое пособие для учителей. — М.: Новая школа, 2006. — 252 с.

26. Зак А.З. Развитие интеллектуальных способностей у детей 9 лет: Учебно-методическое пособие для учителей. — М.: Новая школа, 2006. — 108 с.

27. Занков Л.В. Избранные педагогические труды / Л.В Занков. — М.: Педагогика, 2000. — 424 с.

28. Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах — М.: Просвещение, 1985.

29. Истомина Н.Б. Активизация учащихся на уроках математики в начальной школе / Н.Б. Истомина. — М.: Просвещение, 2006. — 212 с.

30. Крупич В.И. Дидактический механизм возникновения проблемной ситуации в обучении математике /В.И. Крупич. — М.: МГПИ, 2004. — 111 с.

31. Крутецкий В.А. Психология математических способностей школьников.- М.: Просвещение, 2008. — 432 с.

32. Крутецкий В.А. Психология обучения и воспитания школьников / В.А. Крутецкий.- М.: Просвещение, 2006. — 451 с.

33. Кудрявцев Т.В. Исследование и опыт проблемного обучения / Т.В. Кудрявцев. — М.: Высшая школа, 2008. — 89 с.

34. Кудрявцев Т.В. Проблемное обучение: истоки, сущность, перспективы /Т.В. Кудрявцев. — М.: Знание, 2001. — 80 с.

35. Кулько В.А. Формирование у учащихся умений учиться: Пособие для учителей / В.А. Кулько, Т.Д.Цехмистрова. — М.: Просвещение, 2003. — 79 с.

36. Кульневич С.В. Современный урок. Часть 3. Проблемные уроки: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов и аспирантов пед. учеб.заведений, слушателей ИПК. / С.В. Кульневич, Т.П. Лакоценина. -М.: Знание, 2006. — 288 с.

37. Лейтес Н.С. Способности и одаренность в детские годы / Н.С. Лейтес. — М.: Знание, 2004. — 80 с.

38. Лернер И.Я. Проблемное обучение / И.Я. Лернер. — М.: Знание, 2004. — 64 с.

39. Лернер И.Я. Система методов обучения / И.Я. Лернер.- М.: Знание, 2006.- 71 с.

40. Лоповок Л.М. Тысяча проблемных задач по математике: Кн. Для учащихся / Л.М. Лоповок. — М.: Просвещение, 2005. — 86 с.

41. Людмилов Д.С. Некоторые вопросы проблемного обучения математике: Пособие для учителей, Д.С. Людмилов, Е.А. Дышинский, А.М. Лурье. — Пермь, 2005. — 69 с.

42. Максимова В.Н. Проблемный подход к обучению в школе: Методическое пособие для учителей / В.Н. Максимова. — СПб.: Печатный двор, 2003 — 325 с.

43. Рудницкая В.Н. Контрольные работы в начальной школе по математике — М.: Дрофа, 1996.

44. Русова Н. Универсальный справочник для начальных классов — Н. Новгород: Деком, 1996. Давайте поиграем/ Под. ред. À.А.Столяра. — М.: Просвещение, 1991.

45. Тихомирова Л.Ф. Развитие интеллектуальных способностей школьников / Л.Ф. Тихомирова. — Ярославль, 2006. — 240 с.

46. Шамова, Н.В. Активизация учения школьников / Н.В. Шамова.-М.: Просвещение, 2002. — 218 с.

47. Щукина Г.И. Активизация познавательной деятельности учащихся в учебном процессе / Г.И. Щукина. — М.: Просвещение, 2004. — 233 с.

48. Артёмов А.К. Приёмы организации развивающего обучения / А.К. Артёмов // Начальная школа. — 1955. — №3. — С. 35-39.

49. Бантова М.А. Система формирования вычислительных навыков/ М.А. Бантова // Начальная школа. — 2008. -№ 11. — С. 38-43.

50. Белавина И.Г. Психологические последствия компьютеризации детской игры. // Информатика и образование. – 1991. — №3. с. 40

51. Блохин И.А. О проблемном обучении в начальных классах / И.А. Блохин, В.В. Ляхин, В.П. Стрезикозин // Начальная школа. — 1993. -№6. — С. 53-64.

52. Корчемлюк О.М. Задания для развития памяти и внимания на уроках математики / О.М. Корчемлюк // Начальная школа. — 1994. — №8. — С. 26-32.

53. Репкин В.В. Формирование учебной деятельности в младшем школьном возрасте//Начальная школа – 2009 — №7 – с.19 – 24

54. Сухорукова В.М. Интересные приемы устных вычислений // Начальная школа. — 2011. — №6. -с.34.

55. Узорова О.В. Устный счёт и математические диктанты для начальной школы.- М.: Просвещение, 2011.- 234с.

56. Узорова О.В., Нефедова Е.А.. Контрольные и проверочные работы по математике — М.:Аквариум, 1997- с.10, 25. Журнал «Начальная школа».

57. Электронные библиотеки // Москва: Младшая школа – 2005.- ( Рус .) –URL: http://www.mladshyia shkola.net/i2a1a2.asp235616

58. Электронные библиотеки // Москва: Педагогика и психология – 2004.- (Рус.) –URL: http://www.nezachetov.net/i2a1a2.asp?id=19316

59. Электронные библиотеки // Педагогика – 2005.- (Рус.) –URL: http://www.sdal.ru/works/

60. Электронные библиотеки // Педагогика и психология – 2006.- (Рус.) –URL: http://vio.fio.ru/vio_17/cd_site

61. Программа мониторинга уровня сформированности универсальных учебных действий в начальной школе. [Электронный ресурс] URL: .

62. Черкасова И.И., Яркова Т.А. Интерактивная педагогика. [Электронный ресурс] URL: http://tgspa.ru.

ПРИЛОЖЕНИЕ 1

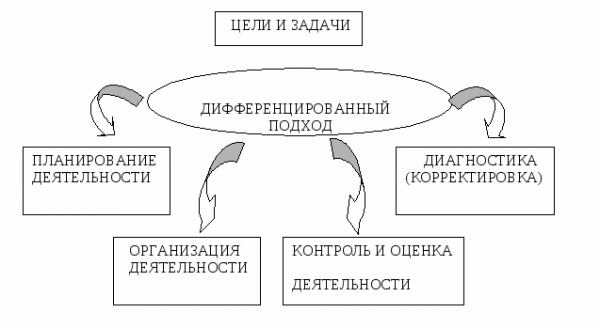
ПРИЛОЖЕНИЕ 2

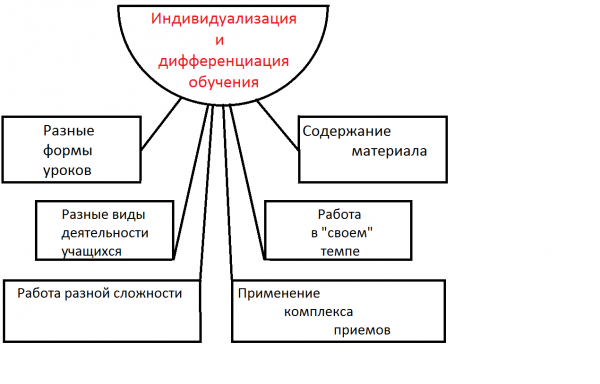
ПРИЛОЖЕНИЕ 3

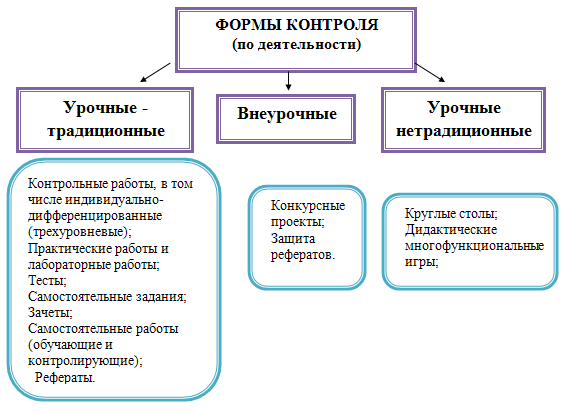
ПРИЛОЖЕНИЕ 4

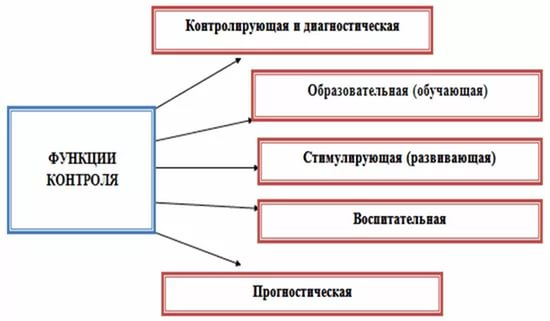
ПРИЛОЖЕНИЕ 5

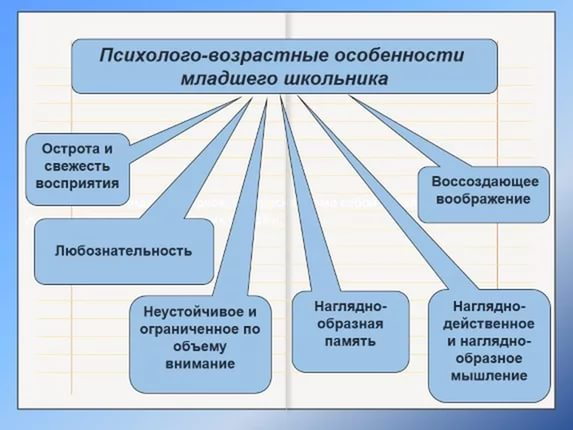
ПРИЛОЖЕНИЕ 6

ПРИЛОЖЕНИЕ 7

ПРИЛОЖЕНИЕ 8

ПРИЛОЖЕНИЕ 9

ПРИЛОЖЕНИЕ 10

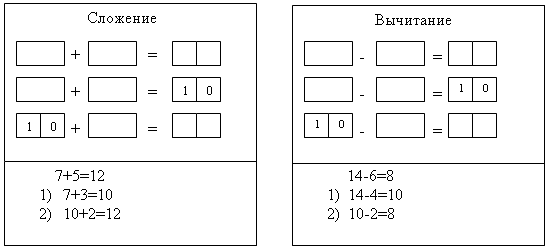
ПРИЛОЖЕНИЕ 11

Игра “ Математические цепочки”.

Например:

А) Детеныши, какого животного еще слепые, а уже умеют защищаться от врагов.

Крот – 1

Еж – 0

Волк – 2

1х7 + 3 – 10 = ?

Б) Это растение каждой бродячей собаке радо. Даже лис, медведей и волков не боится. Они дерут его клыками, когтями рвут, а растение за них цепляется – расстаться с ними не может. Что это за растение?

Мокрица – 3

Молодило – 2

Репейник – 1

8х1 + 2 – 9 = ?

1. «Магический квадрат»:

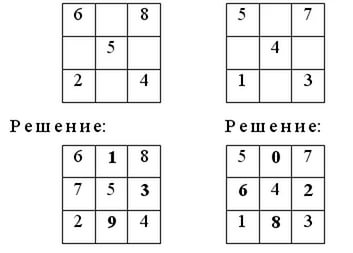
ПРИЛОЖЕНИЕ 12

ПРИЛОЖЕНИЕ 13

Игра “Математическая мозаика”.

У каждого ученика имеется карточка с записанными на ней числами. Учитель диктует задание, ученик считает и закрашивает полученное число, в результате, если все задания выполнены верно, получается цифра 5

Например:

• 5 х 7

• Увеличь 9 в 5 раз

• Первый множитель 8, второй множитель 5. Найди произведение.

• 9 х 9

• Какое число надо умножить на 6, чтобы получить 42

• Уменьши 32 на 4

• Во сколько раз 5 меньше 30

• Делимое 35, делитель 7. Чему равно частное.

• Увеличь 8 в 8 раз

• 8 х 4

• Во сколько раз 45 больше 9

ПРИЛОЖЕНИЕ 14

ПРИЛОЖЕНИЕ 15

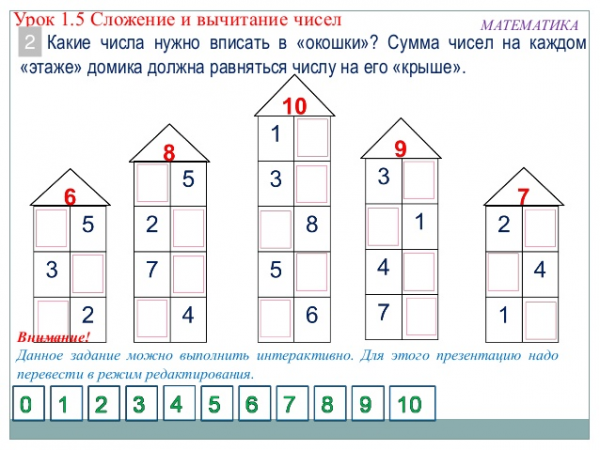
ПРИЛОЖЕНИЕ 16